|
Aligned series |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
John Aach
Last Modified: June 11, 2001
Recently developed high throughput assays for mRNA expression such as DNA microarrays, oligonucleotide arrays, microbeads, and serial analysis of gene expression (SAGE) (Brenner et al., 2000; DeRisi et al., 1997; Lockhart et al., 1996; Velculescu et al., 1995) have enabled researchers to study biological processes systematically at the level of gene activity. Clustering of expression data gathered by these means to functionally characterize genes (Eisen et al., 1998; Tamayo et al., 1999; Tavazoie et al., 1999), and to classify samples and conditions (Aach et al., 2000; Alizadeh et al., 2000; Bittner et al., 2000; Golub et al., 1999) is now commonplace. An important area of application of these techniques is the study of biological processes that develop over time by collecting RNA expression data at selected time points and analyzing them to identify distinct cycles or waves of expression. Progress in the development of high throughput protein level assays (Gygi et al., 2000; Gygi et al., 1999; Futcher et al., 1999) suggests that similar techniques will soon be used in the area of protein expression analysis.
Biological processes have the property that multiple instances of a single process may unfold at different and possibly non-uniform rates in different organisms, strains, individuals, or conditions. For instance, different individuals affected by a common disease may progress at different and varying rates. This presents an issue for analysis of biological processes using time series of RNA expression levels: To find the time point of one series that corresponds best to that of another, it is insufficient to simply pair off points taken at equal measurement times. Analysis of such time series may therefore benefit from the use of alignment procedures that map corresponding time points in different series to one another.
Dynamic time warping is a variety of time series alignment algorithm developed originally for speech recognition in the 1970s (Sakoe and Chiba, 1978; Velichko and Zagoruyko, 1970). Similar to algorithms used for sequence alignment, time warping aligns two time series against each other. Whereas sequence alignment algorithms consider the similarity of pairs of single bases or residues taken one each from each sequence, time warping considers the similarity of pairs of vectors taken from a common k-dimensional space (feature space) taken one from each time series. Here the feature space comprises vectors of RNA expression levels from a common set of k genes. The time warping algorithms developed here are global alignment algorithms; therefore Needleman-Wunsch presents the most analogous sequence algorithm (Needleman and Wunsch, 1970). While in its most general form time warping makes no assumptions about the evenness or density of data sampling in the time series it aligns, simplifications and efficiencies are often possible when sampling rates are constant and of high density. These conditions are easily met when sampling speech data through appropriate electronics and data processing, but not for RNA expression level data where collection of data at a time point involves laborious and costly steps. Examples of unevenly and sparsely sampled RNA expression time series are common in the literature, and this will surely be true of protein time series as well. As a result, time warping algorithms developed for speech recognition cannot generally be directly applied to typical expression level time series. To demonstrate time warping on these data, we therefore implemented time warping algorithms for expression data from first principles as described in (Kruskal and Liberman, 1999), including an interpolative algorithm that to our knowledge has never been previously implemented.
In the text of the article, we show that time warping produces alignments that are expected given the series being compared, and explore the impacts of numbers of genes and measurement noise on the stability and quality of alignments. We compare time warping with clustering as a way of mapping corresponding time points, and assess the use of alignment scores in judging the quality of alignments. In discussion we describe potential enhancements to and alternative uses of the algorithms. For instance, the time warping algorithms could also be used to align non-temporal series such as expression profiles for cells over a range of concentrations of compounds (concentration warping); these would be of interest whenever cells have a common dose response trajectory at the RNA or protein expression level but move through it at different rates relative to changes in compound concentration when the cells are from different strains or culture conditions. We also compare time warping with signal analysis techniques such as singular value decomposition (SVD) and Fourier analysis, and call attention to the possibility of time series superpositions -- situations where different pathways move independently of each other and so do not warp in lock-step with each other when compared across different cell lines, strains, or conditions.
The programs genewarp, genewarpi, grphwarp, and grphwarpi were developed in C++ on a 200MHz Pentium II computer with 96 MB RAM running NT 4.0 (Service Pack 3) using Microsoft Visual C++ 6.0 (Microsoft, Redmond, WA) without any Windows-specific features but using the C++ Standard Template Library (STL) (see Stroustroup, 1997). The programs should be executable in the DOS box of any Win32 system. Program routines implementing the dynamic programming algorithm (see Algorithm and Implementation) only use C functionality to avoid overhead associated with object management and the STL. At this time, unequal implementation of STL by different compilers has prevented compilation outside of Microsoft Visual C++ despite the avoidance of windows-specific features. Therefore only Win32 executables are currently available.
The four programs work in pairs: genewarp and grphwarp, and genewarpi and grphwarpi. genewarp performs a simple time warping, while genewarpi performs an interpolative warping (see Algorithm and Implementation). genewarp and genewarpi produce a dump file that contains copies of the input and generated alignment information that must be passed to graphics programs grphwarp and grphwarpi for graphics generation. It takes ~ 3 seconds to align time series using genewarp containing the 200 MHz Pentium II, 96MB RAM development machine. Generated graphics contain four parts: graphs of the two input time series in real time, a graph displaying the optimal path through the dynamic programming matrix (see Algorithm and Implementation), and a graph of the alignment of the input series in a time frame where time values of aligned time points are the averages of the aligned input series time point values (the trajectory average time frame in (Kruskal and Liberman, 1983). Sample output may be viewed here. grphwarp and grphwarpi can be instructed to display only specific sets of genes from the input time series and time alignment, a useful feature when the number of input genes is large.
Click here to get copies of Win32 executables for these programs.
|
genewarp |
Performs simple time warping on user-supplied time series |
|
grphwarp |
Generates graphic depiction of genewarp input time series and genewarp-generated time alignments |
|
genewarpi |
Performs interpolative time warping on user-supplied time series |
|
grphwarpi |
Generates graphic depiction of genewarpi input time series and genewarpi-generated time alignments |
Details on the alignment algorithms may be found in the article. The algorithms are primarily based on (Kruskal and Liberman, 1983)
genewarp takes two input files and generates all optimal alignments. The input files are specified using the -i1 and -i2 parameters. It produces an output message file and also a "dump" file that contains copies of the input file, program parameters, and information describing the discovered optimal alignment(s). The dump file is fed to grphwarp using the -d parameter and produces graphical depictions of the alignment(s) generated. Similarly, genewarpi takes input files -i1 and -i2 and generates a dump file that may be fed to grphwarpi for graphics generation. genewarp alignments must be graphed using grphwarp, and genewarpi alignments with grphwarpi. No other combination will work.
grphwarp and grphwarpi graphics are generated as PostScript files that may be viewed with GhostView or Adobe Photoshop.
Descriptions of the graphics may be found here.
All four programs have been made available as Win32 executables. They may be executed from DOS command lines on Windows 95, Windows 98, Windows ME, and Windows NT machines.
Each of these programs supports numerous options that are specified by parameters. Parameters are supplied by using a parameter code (e.g., -i1, -i2, -d) followed by a space followed by 0 or more space-separated arguments. E.g., to execute genewarp in a way that specifies the two input series to be aligned, the name of the dump file to be produced, and the output message file, the following may be entered on a command line.
Parameter codes are case-sensitive. A complete list of parameters for a program and their specifications may be viewed by executing the program without any parameters at all, or may be viewed by going to the following hotlinks:
Parameters that take 0 arguments are generally logical switches that may be turned off inserting a ~ after the initial - in the parameter code. For instance, the -D switch tells genewarp and genewarpi to produce a dump file to be passed to grphwarp or graphwarpi and is on by default. To turn it off, the code -~D may be supplied.
Some parameter codes are themselves very lengthy expressions, especially many of the parameters that control graphics generation in the graphing programs. However, only a unique prefix need be supplied. E.g., the genewarpi parameter code -enforceorder forces genewarpi to avoid interpolation time point order errors at the cost of generating a possibly sub-optimal alignment (see Algorithm and Implementation for details). It may be supplied simply as -e, since this prefix happens to be unique among its supported parameters.
Because parameter lists may be lengthy they may be all be put in a parameter file which can then be specified using the -p parameter code. Parameter codes and arguments in the parameter file must be specified just as they would be on a command line except that they may be broken out onto multiple lines of the file (allowing them to be more easily read and edited). The -p parameter may be used to provide defaults to the program that may be overridden or augmented by other parameters supplied directly on the command line. If the -p parameter code is found in a parameter file, it is ignored. Examples of parameter files are given here.
Most parameters for the four programs are supplied with usable defaults. The only required parameters are
|
genewarp |
-i1, -i2, -o (-d defaults to the file name specified via -o + ".data") |
|
grphwarp |
-d, -o |
|
genewarpi |
-i1, -i2, -o |
|
grphwarpi |
-d, -o |
Format of the input time series data files
The two input time series must be in a specially devised format that is a variant of FASTA format and which consists of
Each gene name must only be used once in each time series, and, in the current implementation, expression level values must be provided for all time points in the series. The two input time series to a genewarp or genewarpi execution must share exactly the same gene names.
Please cite usage of genewarp, grphwarp, genewarpi, and grphwarpi by
Aach, J. and Church, G. (2001) Aligning gene expression time series with time warping algorithms, Bioinformatics 17(6): 495-508.
Sample selection and parameter files may obtained here:
You might want to be aware of some possible problems that can arise when downloading sample data and parameter files.
To run these files, copy the parameter, data, and selection files to the same directory as the programs. To run genewarp and view its output, execute the following two commands in a DOS box in this directory:
genewarp -p genewarp.parms.txt
Output messages will be in genewarp.alignment.msgs.txt.
grphwarp -p grphwarp.parms.txt
Warning messages will appear for genes named in the selection file that are not in the input data; these are normal and you may ignore them. Output messages will be in grphwarp.msgs.txt, and the output PostScript graphics file will be in grphwarp.graphics.1.ps. The latter may be viewed in GhostView or Adobe Photoshop.
To run genewarpi, use the following commands:
genewarpi -p genewarpi.parms.txt
Output messages will be in genewarpi.alignment.msgs.txt.
grphwarpi -p grphwarpi.parms.txt
Again, warning messages for genes named in the selection file that are not in the input data are normal and may be ignored. Output messages will be in grphwarpi.msgs.txt, and the output PostScript graphics file will be in grphwarpi.graphics.1.ps.
Possible problems downloading or using the sample files
For any other problems, please contact us.
Click on the thumbnail path graphs for any of the alignments displayed below to see a larger image with time series graphics included. Several of these alignments are discussed in detail in the article. Also, go here for a general description of alignment graphics.
Small cluster alignments
These are alignments that involve small numbers of genes. As noted in the article, the shape of small cluster path graphs does not tend to be stable across clusters.
|
Aligned series |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Large gene group alignments
As demonstrated in the article, these are more stable than small gene cluster alignments. The pgt50 gene group generated the most stable alignments. Only alignments of the alpha and cdc15 series are shown.
|
Aligned series |
|||
|
|
|
|
Half series alignments
These are alignments of the first half of each cell cycle time series against the second half. Both the alpha and cdc15 series have ~2 periods and therefore their half series align well. The elu series contains only ~1 period and its half series show complete non-alignment. See Half cell cycle series alignments for additional details.
|
Aligned series |
|||
|
half 1 vs. half 2 |
|
|
|
Interpolative alignments
These are alignments that either use an interpolative time warp algorithm or which use simple (non-interpolative) alignments on time series with interpolated time points. Go here for a full discussion of interpolative time warping. Only alignments using the pgt50 gene set and the alpha and cdc15 series are shown. The enforceorder option prevents interpolation time point order errors at the price of generating a possibly suboptimal alignment. The simple (non-interpolative) alignment with interpolated time points used time series that were modified by the insertion of new time points interpolated halfway between each pair of consecutive time points in the original series.
|
Algorithm |
interpolative |
interpolative with enforceorder |
simple with interpolated time points |
|
|
|
|
In the Spellman, et. al. experiments synchronized Saccharomyces cerevisiae cell cultures exhibited periodic behavior and the problem was to identify which of the ~6000 genes had expression profiles with corresponding periodicity. To do this, the authors computed the following values for each gene in each of their synchronized cell culture time series (plus a series from another study):
A =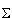 
sin(
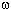t +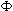 
)log2(expression(t))
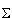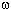B = cos( t + 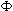)log2(expression(t))
C = (A,B)
D=(A2+B2)1/2
Here 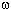= frequency, 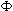= phase, expression(t) = the
ratio of the expression level of the gene in the synchronized culture to its level in a parallel
control unsynchronized culture at time t, where the log2(expression(t)) values are
normalized so that they sum to 0 over the course of the series. is
set to 0 initially and D is computed over a range of values for
each series, but ultimately values are computed that allow three
series to be combined by weighted addition of their C vectors, and a D computed
from this aggregated C (here called the aggregated D). Within each series,
D is a measure of the magnitude of the first Fourier coefficients for frequency
, and thus a measure of the gene's periodicity. To improve stability of
D values over small shifts in , what was actually considered was an
average of the C values over a window of 40 values centered
on the one of interest. A threshold for aggregated D was set based on genes known to be
cell cycle regulated, resulting in identification of 800 candidate cell cycle-regulated genes.
This method allowed identification of genes which showed periodic behavior in
accordance with a cell cycle whose frequency was estimated directly. We decided to
reverse the method and estimate the cell cycle frequency of each series by looking at
the values that maximized D for each of the identified genes.
Specifically, we first generated a list of 767 genes that were identified as periodic on
the Spellman, et. al. experiments web site
and which we could identify with Saccharomyces Genome Database IDs
on our own expression database ExpressDB.
Then, for each of the alpha, cdc15, and elu
series, we computed D values for each of these 767 genes for a series of
values corresponding to a series of cell cycle periods between a specified minimum and
specified maximum time value separated by 0.5 minute each. As in the original method, we computed a
window-averaged C value for each period value by averaging the C values for the 41
values centered on the given period. (For periods were near the maximum and minimum of the
period range we were forced to average fewer values). We then computed Ds for each period
value based on these window-averaged Cs, and identified the period with the maximum D value
(here called maxDp).
We found that the distribution of maxDp values over the 767 genes could contain large numbers of outliers. For instance, for the alpha series, we found that when we computed maxDp based on an period range between 25 and 75 minutes (which spans at least 9 minutes on either side of the reported period of 66 +/- 11 minutes), we found that 46.7% of the 767 periodic genes had a maxDp = 75 minutes and 1.2% had a maxDp = 25 minutes, the maximum and minimum period of the specified range, respectively. This meant that 47.8% of the genes had maxDp values that could not be believed reliable since they would likely exhibit even higher D values for period values outside of the computed range, and, as a result, the average and standard deviation of the maxDp values (68.4 +/- 10.1) could likewise not be believed reliable. The situation could be improved by increasing the range of period values to span from 20 to 90 minutes, but even here 18.3% of the 767 genes were found to have maxDps at the extremes of the range. The situation was worse for the cdc15 and elu series. Moreover, not only did the distribution of maxDps contain large numbers of outliers but the shape of the distribution was not unimodal and smooth but multimodal and irregular.
It is not uncommon to find genes in microarray-based expression data series for which values are not reported for one or more condition due to failure of the expression level measurement to pass quality tests. In the present case this shows up as genes which have no reported value for one or more time points among the three series. In the context of the Fourier calculation above, missing time point values have the same effect as having 0 values at that time point and can introduce error into the calculation of a gene's period. To see whether the presence of genes with missing values was leading to the large number of outliers in the maxDp distribution, we computed maxDps for the alpha series based on the 20 to 90 minute period range for the 591 genes among the 767 that contained no missing values. However, even with these genes with missing values removed, 17.9% of the 591 remaining genes still had maxDps at the extremes of the period range.
We decided that the best procedure would be to compute cell cycle periods based on the medians of the maxDp distributions since these are independent of the exact (uncalculated) values of the maxDp outliers so long as fewer than 50% of maxDp values are found to be at either the maximum or the minimum of the period range. This led to the computed period values shown in Table 2. To compute the error values in Table 2, we computed the median of the absolute value of the differences between all maxDp values and the median maxDp. This value will be stable and independent of maxDp outliers so long as fewer than 25% of maxDp values are found to be at either of the range extremes. We found we could satisfy this latter condition for the alpha and cdc15 series, but not for the elu series. For this latter series we found 36.5% of the maxDp values were at or greater than the maximum period, even when this maximum period was 500 minutes. We therefore report the elu period 77.5 minute error value as an underestimate of the variability of the computed elu cell cycle period.
The cell cycle period values computed by these means are in reasonably good accord with information published in the Spellman et. al. (1998) article, although our computed periods tend to be longer. The article reports a 66 +/- 11 minute period for alpha vs. our 67.5 +/- 6.5. For cdc15 we found a 119.0 +/- 14 minute period whereas the article reports ~3 cycles for this series in 290 minutes (about 96.7 minutes). For elu we found a 422.5 +/- 77.5+ minute period whereas the article reports ~1 cycle in 390 minutes.
We developed a simple and an interpolative algorithm described in (Kruskal and Liberman, 1983). Let the two time series to be aligned be a and b. Series a has time points 0, 1, ..., n at times t0 < t1 < ... < tn, and series b has time points 0, 1, ..., m at times u0, < u1 < ... < um. In the present case, each of the two series is associated with a set of k genes for which expression level values are provided over the course of the series. However, in this and the section below we use more general terminology and refer to the series as being associated with a trajectory of feature vectors in k-dimensional feature space. We denote the feature vector for series a at time point ti by ai and the b series vector at time uj by bj. Series a and b may each be viewed as sampling a process that sweeps out a trajectory in feature space over time. Broadly speaking, time warping finds the correspondence between the time points of each series that minimizes an overall distance D(a,b) between trajectories while maintaining the order and continuity of each time series. A depiction of two aligned time series in a two-dimensional feature space is given in Figure 1a. In both the simple and interpolative algorithm, the constraints of order and continuity are defined by reference to permissible paths (known as warping paths) through a table in which time points from one series are laid out in order along the horizontal axis and time points from the other along the vertical. Specifically, for simple warping, we consider paths defined by functions i(h) and j(h) that, for h = 0,1, ... , p, specify time points in the a and b series, respectively, and where
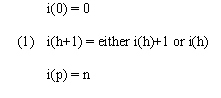
and similarly for j(h). The warping path corresponding to Figure 1a is shown in Figure 1b. In general, time warping algorithms find the warping paths that minimize overall trajectory distance by dynamic programming. Different definitions of overall trajectory distance and additional or varied constraints on warping paths yield different varieties of time warping algorithms.
In the simplest algorithms, overall distance along an initial segment of a warping path is defined as
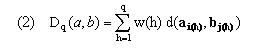
The overall distance D(a,b) along the entire warping path is then Dp(a,b). Here d(x,y) provides a measure (see (6)) of the degree of separation of vectors x and y in feature space and w(h) provides time weights that adjust for the length of the path through the table and also ensure invariance over further warping of the uniform time frame implicitly defined by h. Following Kruskal and Liberman, we take
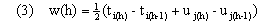
Here, w(h) represents the average time spent in the two trajectories defined by a single move along the warping path. We base distances for all of our algorithms on weighted euclidean distance
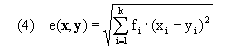
for k-dimensional feature vectors x and y and feature weights fi, where these weights may be specified as parameters; however, all work presented here and in the article uses fi = 1 for all genes. Use of euclidean distance is the source of our current implementation requirement that values must be available for every time point for every gene in the input time series. An alternative that could be used where x and y are missing small numbers of values would be
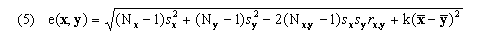
where Nx, Ny, and Nx,y are the numbers of
coordinates in the two vectors and the number present in both, sx
the sample standard deviation of the x coordinates present (similarly for y),
rx,y the sample Pearson correlation coefficient of x and
y over the coordinates present in both, and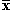 
the average value of
the coordinates present in x (similarly for y). If we were to use
e(x,y) directly for d(x,y) in (2), the time weight for each
warping path segment would be applied to the distance d obtained from the feature vector
of each series at the right endpoint of the segment; we call such an algorithm a
right-endpoint algorithm. In genewarp we use more symmetric alternative given by
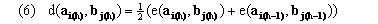
(average-endpoint algorithm), although genewarp may be instructed to use a right-endpoint algorithm by a parameter. The dynamic programming recursion in genewarp considers the cells indicated in Figure 1c, i.e. to find the optimal partial warping path(s) to the cell with coordinate (i+1,j+1) it finds the cell(s) with coordinates (i,j), (i+1,j), and (i,j+1) whose partial paths, when extended to (i+1,j+1), result in a minimal partial distance Dq(a,b). genewarp returns both the optimal paths and also the value D(a,b) (optimal alignment score). Execution time of the simple warp algorithm is O(mnk) while its memory requirement is O(c1mn + c2k(m+n)) for appropriate constants c1 and c2.
In time warping, vertical or horizontal segments of a warping path represent time
compressions or expansions (compexps) in which a time point in one series is mapped to multiple
time points in the other (e.g., time point 1 in series b in Figure 1b,
which corresponds to u1 in Figure 1a). Compexps correspond to
insertion / deletions (indels) in sequence alignment. However, compexps are scored like any other
segments of a warp path by summing w(h)d(ai(h),bj(h)) terms while
indels are scored using a gap scoring scheme based on gap initiation and extension costs that is
different from the base or residue similarity scoring used elsewhere in the sequences.
Where the underlying processes sampled by time series are continuous or nearly so, compexps artificially
represent process segments that span continuous intervals of time as jumping instantaneously at a point
in time. Compexps may also result in artificially inflated overall path distances D(a,b).
Use of interpolations between time points can address these issues. One option is to apply simple warping
to time series which have been supplemented with interpolated values. The genewarp and grphwarp programs
can be used directly on such interpolated time series.
In this method, compexps still appear in warps of interpolated time series but may represent smaller time intervals,
and computed path distance values will be based on comparisons of interpolated time points that do not
represent actually measured values. For situations where these characteristics are undesirable, Kruskal and Liberman
describe an interpolative algorithm that helps minimize them. In this algorithm, a warp path is built up from time
points that include both time points actually provided in the series (sample points) and interpolations between
consecutive time points in the series: Each step of the warp path aligns a sample point in one series to an
interpolated point in the other, where the interpolated point represents the point on the line in feature
space between the two consecutive time point feature vectors that is closest to the sample point vector in the first
series. This situation is depicted in Figure 1d. We denote by (i,(j,r)) a mapping of time point i from series a to an interpolated
point u(j,r) whose time value is (1-r)
uj+ruj+1 with
0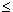
r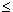1 in series b, and similarly for ((i,r),j). We call r the interpolation
value. The feature vector b(j,r) at u(j,r) point is (1-r)bj + rbj+1.
Warping paths are built from functions i(h) and j(h) where h = 0, 1, ... , p, where i(h) = z or (z,r) for
integer z between 0 and n and 0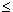r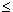1. In the first case, i(h) is a sample point and
the second it is an interpolated point. We then have
and similarly for j(h). Although r values in the path differ from node to node along the warping path, we henceforth simplify notation except where needed by simply referring to them all with the same variable r instead of different variables for different nodes (as we did with r' vs. r above). We implemented the interpolative algorithm in program genewarpi. Execution time of the interpolative warp algorithm, like that of the simple algorithm, is O(mnk) while its memory requirement is also O(c1mn + c2k(m+n)) for appropriate constants c1 and c2. Examples of interpolative alignments can be found here.
Implementation of the simple time warping algorithm in genewarp was straightforward, but the situation was more complex for the interpolative algorithm in genewarpi. In this apparently first implementation of this algorithm we had to address the following issues:
Graphical depiction: It is convenient to label the intersection points of the dynamic programming grid with time point coordinates as in Figure 1e, rather than the centers of the grid cells used for the simple algorithm (Figure 1b). This makes every step of a warping path a move from either the lower or left edge of a cell to the upper or right edge of the same cell. Distances along the lower or left edge from the time point coordinate intersection point in the lower left corner depict the r values of the current interpolation point.
Time weights and path distances: Kruskal's and Liberman's algorithm assumes constant sampling which enables it to use constant time weights. We therefore had to develop alternatives. A requirement for time weights is that they should sum to a constant over all possible warping paths. The simplest possibility is given by what we call categorical time weights:
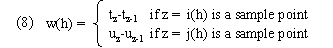
These are categorical in the sense that they are determined by the categories of time points aligned at warp path node; in particular they depend only on the time values of the sample point and ignore the time values of the interpolation point. We call time weights given by (3) interpolative time weights; these depend on both kinds of time points as well as the interpolation values at the current and preceding time point alignments. Our distance function d(x,y) remains as in (6) (average-endpoint algorithm). (As with genewarp, genewarpi may be instructed to use a right-endpoint algorithm by a parameter.) D(a,b) is given by (2).
Dynamic programming recursion: Dynamic programming matrix element (i,j) must keep track of two
distinct sets of data, one for the case when i is the sample point and the other for when j
is the sample point. This is depicted in Figure 1f. The matrix element being filled in is
(i+1, j+1) and it is the intersection point at the center of the grid. The point * represents the case
where j+1 is the sample point;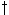 
represents the case where i+1 is the
sample point. In each case, the sample and interpolation point of a previous cell is examined
and the path(s) which generate a minimal partial score are kept, e.g., extensions from
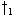and 
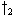to 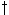in Figure 1f
are each considered and the one yielding the minimum partial score is retained
for .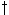
Interpolation alternatives: In genewarpi, r is chosen for ((i,r),j) so that
e(a(i,r),bj) is minimized. When interpolative time weights are used
w(h) and d(ai(h),bj(h)) both depend on r and another possibility
is to choose an r that minimizes the product w(h)d(ai(h),bj(h)). This
value represents the actual dynamic programming score increment for a path extension, and an interpolative
algorithm that used such r values would generate alignments with smaller scores and thus better
interpolative alignments than one which minimized d(ai(h),bj(h)) values alone.
Different minimizations are required depending on whether a right-endpoint or average-endpoint algorithm is
used. However, such algorithms are refractory to dynamic programming because extensions from the two
partial warp path endpoints in a previous cell may lead to different r values in the current one. E.g., in
Figure 1f 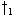and 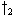may extend to
different points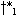 
and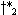 
and not to a common
, and the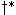 
that minimizes the score in this extension
may not generate the lowest scoring path in the next extension. These complications do not arise for
categorical time weights.
Reduced optimal paths: From the perspective of the algorithm ((i,1),j) is not identical to
(i+1,(j,0)) but from a graphical perspective they are; similarly for (i,(j,1)) and ((i,0),j+1). Under
suitable conditions the algorithm may discover multiple optimal paths through the dynamic programming matrix
that differ only in such graphical synonyms. To avoid generation of multiple identical graphics, genewarpi
generates a set of reduced optimal paths in which graphical duplicates are eliminated. In reduced optimal
paths nodes ((i,r),j) and (i,(j,r)) are represented as (i+r,j) and (i,j+r) respectively, and path steps
between synonyms such as ((i,1),j)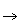
(i+1,(j,0)) are eliminated. The mapping of time points t2 and
u1 in Figure 1d depicts such a situation, the double arrow between them
really consisting of two single but opposed arrows.
Interpolation time point order errors: By picking interpolation points through simple minimization of distances e(a(i,r),bj), nothing prevents the algorithm described here from violating time warp order constraints by finding two interpolation points in a row the second of which occurs earlier in the time series than the first. This can happen when one of the time series doubles back in feature space as illustrated in Figure 2. As the order errors only affect interpolation points, optimal alignments containing them may yet be suitable for many purposes. We provide users a way to suppress order errors by running genewarpi with the special parameter enforceorder. When used, whenever the algorithm computes an interpolation ((i,r'),j+1) for a path extension from ((i,r),j) and finds r' < r, r' is updated to r. Alignments returned by genewarpi with enforceorder may not be truly optimal since a better choice of interpolation points might involve lowering r in addition to or instead of raising r'. The true optimum is not easily found through dynamic programming because finding the optimal r would entail looking ahead in the time series for possible order violations that could arise many extension steps later. However, when order violations arise, the true optimal D(a,b) will be between the score returned for the alignment containing the order errors and the score returned with the enforceorder option.
It was shown in the main article that time warping produces expected results when used to align the pgt50:alpha and pgt50:cdc15 time series. But the alpha series contains nearly two full periods of the cell cycle and the cdc15 series contains slightly more than two (Table 2). An additional test of time warping would be to see if it could map the first and second cycles of each of these two series. As in the case of the pgt50:alpha to pgt50:cdc15 mapping, if warping were perfect we should expect to see an optimal warping path be close to a line of slope 1 (see main article). Results of genewarp alignments are in Half series alignments. In these alignments, the complete set of time points for a single series is divided to make two time series for the same set of genes, and these two half series are aligned against each other. Both the alpha and cdc15 results are close to expectations for perfect warping, containing long segments of close to slope 1. Both alignments also exhibit vertical segments near the ends of the warping path similar to those seen in the full pgt50:alpha to pgt50:cdc15 alignment (see main article). The cdc15 series may be additionally affected by having time points at the beginning and end of the series that are more widely spaced than those in the interior which we would expect to compexp against their counterparts in the other half series and lead to some vertical segments at the beginning and horizontal segments at the end. The elu series contains less than a full cell cycle period (Table 2) so its two halves should not align; in fact they should be nearly completely out of phase with genes at time points in the first half being in nearly opposite cell cycle states compared to corresponding points in the second half. It may thus serve as a negative control that should not exhibit a graph featuring the slope 1 segments expected in good alignments. In fact, the warping of the elu half series exhibits a perfect non-alignment: the entire first half of the series is compexed against the first time point of the second half, and then the second half series is compexed against the last first half time point (see Half series alignments).
|
Series code used in article |
Synchronization technique |
Time points |
|
alpha |
alpha factor |
18 time points from 0, every 7 min |
|
cdc15 |
cdc15-ts |
10, 30, 50, 70, then every 10 min to 250, then 270, 290 (24 time points) |
|
elu |
elutriation |
14 time points from 0, every 30 min |
Table 1.
Series codes and series characteristics of synchronized cell RNA expression time series from Spellman et. al. (1998) used in this study. Table 1 is an abridged form of Table 1 from the article.|
Series |
Cell cycle period (a) |
Periods in series (b) |
Periods / time point (c) |
Initial phase |
|
alpha |
67.5 +/- 6.5 |
1.8 |
0.10 |
G1 |
|
cdc15 |
119.0 +/- 14.0 |
2.4 |
0.08 |
Late M |
|
elu |
422.5 +/- 77.5(e) |
0.9 |
0.07 |
G1 |
Table 2.
Periods and related information for time series used for demonstration of time warping. (a) Cell cycle periods and errors computed from RNA expression data as described here and in article. Values are in minutes. (b) Periods represented in entire time series (see Table 1). (c) Periods represented by interval between consecutive time points. For the cdc15 series the interval was taken to be 10 minutes. (d) Cell cycle phase of series at time 0 as per original reference. (e) Error value presented for elu series is an underestimate. Go here for additional details. This table is identical with Table 2 from the article.|
Gene subsets |
Description |
Usage |
|
pgt50 |
Non-null genes in both the alpha and cdc15 series with variances > 50th percentile in both series individually and together, sorted in descending order by combined series variance (990 genes). |
alignment stability testing time series used for most algorithm testing |
|
pgt33 |
Same as alpha/cdc15-pgt50 except for use of a 33rd percentile threshold (1459 genes). |
alignment stability testing |
|
pgt33-990 |
Last 990 genes of alpha/cdc15-pgt33, containing genes with combined series variance percentiles > 33 and <= 80.1. |
alignment stability testing |
|
pgt50-odd, pgt50-even |
Division of pgt50 where each subset contains every other gene. These sets have approximately the same variance distribution as pgt50 but half the sample size (495 genes). |
alignment stability testing |
|
elu-pgt50 |
Non-null genes in the elu series alone with variances > 50th percentile (2883 genes). |
elu half series alignment |
|
MET, CLB2, CLN2 |
Genes from the MET, CLB2, and CLN2 clusters identified in the original Spellman reference that are non-null in each of the alpha, cdc15, and elu series (11, 27, and 22 genes, respectively). |
alignment visualization small cluster alignments |
Table 3.
Subsets of genes employed in time warping experiments. Non-null genes are genes for which expression levels were available in the original Spellman reference data for every time point in the time series under consideration. This table is a slightly modified form of Table 3 from the article.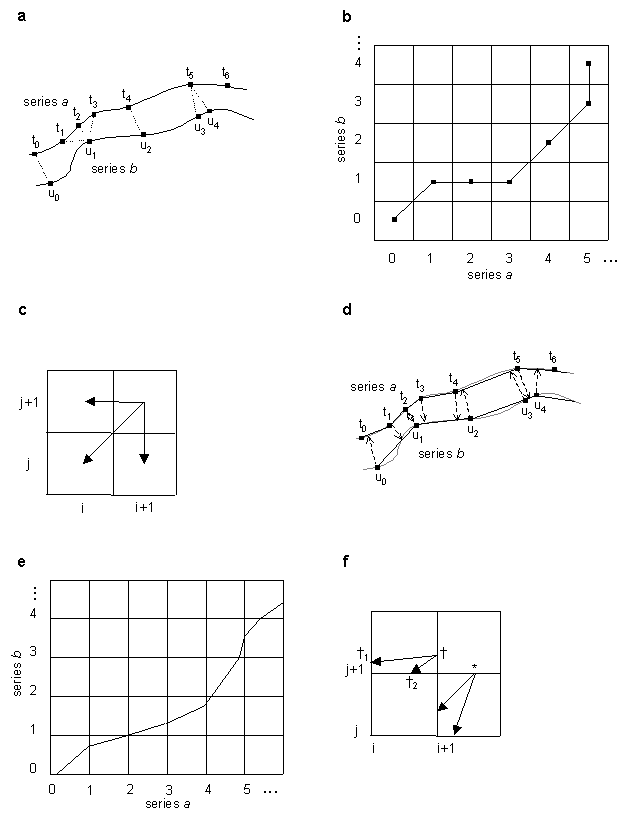
Figure 1. Illustration of simple and interpolative time warping algorithms (see
Algorithm and Implementation for details).
(a) Two time series a and b in a two-dimensional feature space containing
sample points from a continuous process, with sample points of each series mapped to
each other by simple time warping. (b) Dynamic programming matrix for simple warping and the
optimal path corresponding to (a). (c) Path extensions considered by dynamic programming
algorithm in simple warping. (d) Series a and b from (a) with sample
points on each series mapped to interpolative points on the other by interpolative
time warping algorithm. (e) Dynamic programming grid for interpolative warping and the
optimal path corresponding to (d). (f) Path extensions considered by dynamic programming
algorithm. * and are points in cell (i+1,j+1) that correspond to
the sample point in this cell being in series b and in series a, respectively.
and , points in cell (i,j+1) from which
extensions to are computed.
This Figure 1 is an expanded version of the Figure 1 in the article text.
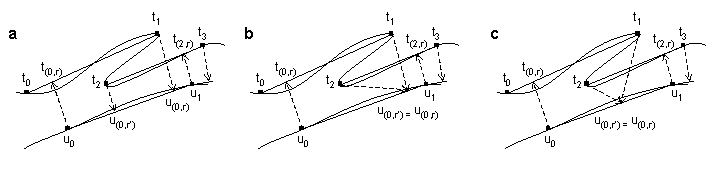
Figure 2. Illustration of interpolation time point order errors. (a) Time series a doubles back in feature space so that the interpolation in time series b from series a time point t2 is closer to series b sample point u0 than earlier time point t1. (b) Illustration of action caused by genewarpi enforceorder option that suppresses order errors. The interpolation from t2 is forced to the larger interpolation point corresponding to the earlier t1. This prevents order errors but may not generate a truly optimal path. (c) A truly optimal path. Here an interpolation value is found intermediate between those found in (a) that optimizes path extension over both sample points while preserving order constraints.
Please feel free to contact John Aach with questions, problems, or concerns.
Copyright (c) 2001 by John Aach and the President and Fellows of Harvard University
